1.1 整数的基础
...大约 2 分钟
整数分为:
- 无符号数:所有位用于表示数字
- 有符号数:最高位表示符号,1(负)0(正)
n 位二进制表示的整数范围:
- 无符号:[0, ]
- 有符号: [, ],整数在计算机中采用补码表示
1.1.1 问题
输入2个int型整数,进行除法运算后返回商。不得使用乘号(‘*‘),除号(‘/’)和求余符号(‘%’)。溢出时返回整数最大值。假设除数不为0。
例:输入15和2,输出15/2,结果为7
1.1.2 分析
流程
可基于减法来进行除法运算,使用被除数减去除数后,将结果与除数比较,若大于则继续,否则商就是计算结果(实际上为除法的计算原理)。
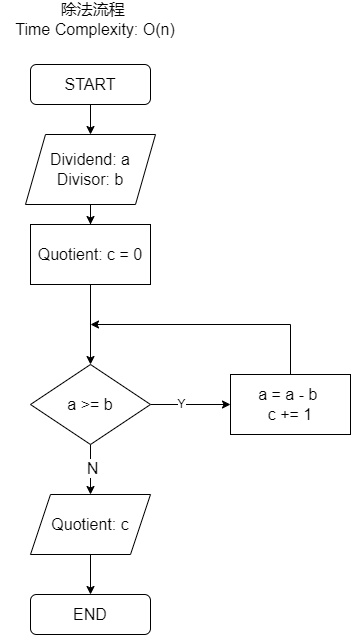
但是上述流程,当除数为1时,时间复杂度达到O(n),故需进行优化。
优化
在判断被除数大于除数时,可进一步判断是否大于其2倍,4倍...乃至2^k倍。即满足(b为被除数):
之后再按减法流程进行,此时时间复杂度为O(logn)。

符号
商的符号取决于被除数和除数,所以结果的正负在计算之前即可得出。
计算时,若将其全部转为正数计算,当数字为最小负整数时,转换成正数会导致溢出(有符号整数范围 [, ],无法表示)
所以计算时需要将其全部转换成负数计算。
边界
由于除数不为0,所以溢出的情况只有一种,即 ,此时结果将超出最大的整数范围。
1.1.3 题解
根据上述的分析可得出流程:

package soint
import (
"math"
)
func divide(dividend, divisor int32) int32 {
if dividend == math.MinInt32 && divisor == -1 {
return math.MaxInt32
}
negative := 2
if dividend > 0 {
negative--
dividend = -dividend
}
if divisor > 0 {
negative--
divisor = -divisor
}
result := divideCore(dividend, divisor)
if negative == 1 {
return -result
}
return result
}
func divideCore(dividend, divisor int32) int32 {
var quotient int32
quotient = 0
for dividend <= divisor {
u := divisor
var v int32 = 1
for divisor >= (math.MinInt32>>1) && dividend <= u+u {
u += u
v += v
}
quotient += v
dividend -= u
}
return quotient
}
Reference
Powered by Waline v2.15.2
