2.2 双指针
双指针是一种常见的解题思路, 通过相反或相同的方向来扫描数组以达成解题.
2.2.1 问题06: 排序数组中的两个数字之和
输入升序排列的数组和一个值k,在数组中找出两个元素之和等于k的元素的下标并返回; 假设数组中只存在一对符合条件的元素, 且单个元素不能使用两次.
例: [1, 2, 4, 6 ] 和 8, 返回[1, 3]
2.2.1.1 分析&题解
暴力解法
遍历数组, 将元素两两匹配求和.
时间复杂度: O()
func twoSumBruteForce(ints []int, n int) []int {
for i := 0; i < len(ints); i++ {
for j := i + 1; j < len(ints); j++ {
if ints[i]+ints[j] == n {
return []int{i, j}
}
}
}
return []int{}
}
二分查找
遍历数组, 对于数字i, 使用二分法寻找 k - i.
二分查找时间复杂度: O(logn)
总体时间复杂度: O(nlogn)
func twoSumBinarySearch(ints []int, n int) []int {
for i := range ints {
t := n - ints[i]
j := binarySearch(ints, t)
if j != -1 && i != j {
return []int{i, j}
}
}
return []int{}
}
func binarySearch(ints []int, t int) int {
left := 0
right := len(ints) - 1
for left <= right {
mid := (left + right) / 2
midVal := ints[mid]
if t == midVal {
return mid
}
if t > midVal {
left++
}
if t < midVal {
right--
}
}
return -1
}
HashTable
- 将数组元素记录于哈希表中
- 遍历数组, 对于数字
i, 在哈希表中寻找k-i(哈希表查找时间复杂度O(1))
时间复杂度: O(n), 空间复杂度: O(n)
func twoSumHashTable(ints []int, n int) []int {
m := make(map[int]int, len(ints))
for i, v := range ints {
m[v] = i
}
for i, v := range ints {
if val, isPresent := m[n-v]; isPresent {
if i != val {
return []int{i, val}
}
}
}
return []int{}
}
双指针
由于数组是有序的, 故可以使用双指针, 假设为升序:
- 左指针(l), 右指针(r) 分别从两端开始反向移动
- 计算两数之和,
- 大于k: 右指针左移
- 小于k: 左指针右移
- 等于k: 返回结果
时间复杂度: O(n), 空间复杂度: O(1)
func twoSumTwoPointer(ints []int, n int) []int {
left := 0
right := len(ints) - 1
for left < right {
sum := ints[left] + ints[right]
if sum == n {
return []int{left, right}
}
if sum > n {
right--
}
if sum < n {
left++
}
}
return []int{}
}
Benchmark
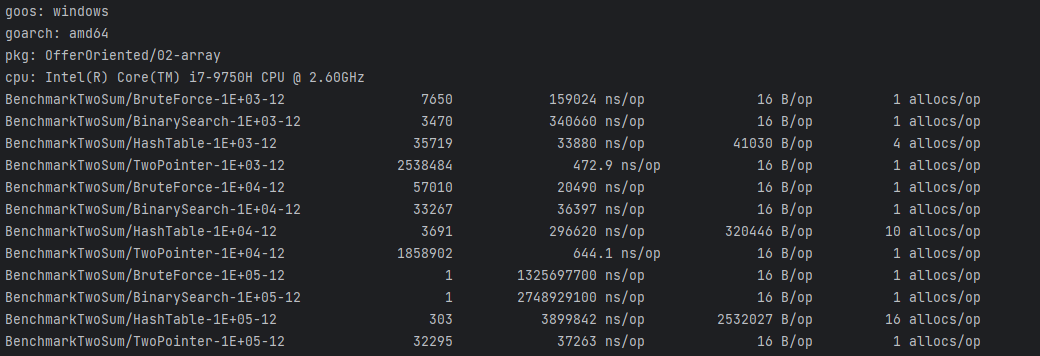
2.2.2 问题07: 数组中和为0的3个数字
输入数组, 找出数组中所有和为0的3个数字的三元组. 返回值不得包含重复的三元组
例: [-1, 0, 1, 2, -1, 4], 返回 [-1, 0, 1], [-1, -1, 2]
2.2.2.1 分析&题解
三数之和为0, 可将其转化为两数之和的问题, 即对于数字 k, 在数组中寻找和为 -k 的数字.
去除重复三元组, 对于满足条件的三元组: [a, b, c], 只要原数组进行排序, 那么一定有 , 只会出现一个三元组 [a, b, c] (不会有 [a , c , b], [b, c, a]...)
流程
- 将原数组进行排序, TC: O(nlogn)
- 遍历数组, 对于元素 i :
- 使用双指针方法找出两数之和为 -i 的元素 j 和 k
- 指针跳过所有的相同元素, 避免重复, 跳过相同元素 i, j 即可. (三元组 [i, j, k], 因为三者之和为0, 那么可以视作[i, j, -i-j], 只需要 i, j 不重复那么三元组就不会重复 )
总体时间复杂度为: O(nlogn) + O() 即 O()
func threeSum(nums []int) [][]int {
// qSortArr array in ascending order
sort.Slice(nums, func(i, j int) bool {
return nums[i] < nums[j]
})
result := make([][]int, 0)
// threeSum
for i := 0; i < len(nums); {
result = twoSum07(nums, i, result)
// skip identical element
ie := nums[i]
for i < len(nums) && nums[i] == ie {
i++
}
}
return result
}
func twoSum07(nums []int, i int, result [][]int) [][]int {
// skip i
left, right := i+1, len(nums)-1
for left < right {
sum := nums[i] + nums[left] + nums[right]
if sum < 0 {
left++
}
if sum > 0 {
right--
}
if sum == 0 {
result = append(result, []int{nums[i], nums[left], nums[right]})
// skip identical nums
le := nums[left]
for left < right && nums[left] == le {
left++
}
}
}
return result
}
2.2.3 问题08: 和大于或等于k的最短子数组
输入一个正整数组和正整数 k , 求数组中和大于或等于 k 的连续子数组的最短长度, 若不存在则返回0
例: [5 1 4 3]和7, [4, 3] 符合条件, 那么最短长度为 2
2.2.3.1 分析
子数组有一个或多个连续数字组成, 那么一个数组可以由两个指针表示.
对于子数组 sub, p1 指向第一个数字, p2 指向最后一个数字, 那么子数组就是由 p1 到 p2 之间的数字组成.
对于子数组之和, 因为元素均为正整数
- p1 右移时, 元素减少则和减少.
- p2 右移时, 元素增加则和增加.
通过一次遍历 (以 p2 进行遍历), 即可寻找出最短的符合条件的连续子数组
2.2.3.2 流程
- 指针 p1, p2 都指向第一个元素
- 计算指针之间的元素之和 sum:
- sum < k, 需增加元素 p2 右移, 和增加
- sum >= k, 满足条件, 更新最小长度, p1 右移, 移除一个元素(和减小), 直到 sum < k
- 流程结束, 返回最小长度, 否则返回0
因为两个循环中, left, right 只增加不减小且均从 0 增加到 n-1, 故时间复杂度为 O(n)
func minSubArrayLen(nums []int, k int) int {
// two pointers
left, right := 0, 0
minLen := 0
sum := 0
for ; right < len(nums); right++ {
sum += nums[right]
for left <= right && sum >= k {
minLen = minLength(minLen, right-left+1)
// next sub
sum -= nums[left]
left++
}
}
return minLen
}
func minLength(m, l int) int {
if m > 0 {
if l < m {
return l
}
return m
}
return l
}
2.2.4 问题09: 乘积小于k的子数组个数
输入正整数组和正整数k, 输出乘积小于k的连续子数组的个数
例: [10 5 2 6] and 100, 满足条件的有 [10], [5], [2], [6], [10 5], [5 2], [2 6], [5 2 6], 输出: 8
2.2.4.1 分析
和前一个问题类似, 使用双指针解决.
对于一个连续子数组 [n1 n2 ... ni], 若元素乘积小于 k, 那么其所有子数组的乘积一定小于 k 且满足条件的长度大于1的子数组个数就为 数组长度
例如: [5 2 6] 和 100, 满足条件的子数组为 [5 2] [2 6] [5 2 6] 为 3 个
2.2.4.2 流程
- 指针 p1, p2 从第一个元素开始
- 计算元素乘积 prod :
- prod < k, 子数组的个数就是数组长度, p2 右移, 积增大, 直到 prod >=k
- prod >= k, p1 左移, 积减小
func numSubarrayLessThanK(nums []int, k int) int {
left, right := 0, 0
count := 0
prod := 1
for ; right < len(nums); right++ {
prod *= nums[right]
for left <= right && prod >= k {
prod /= nums[left]
left++
}
if left <= right {
count += right - left + 1
}
}
return count
}
