15.4 并查集
并查集是一种树形的数据结构, 用于表示不相交集合的数据.
并查集中每一个子集是一棵树, 每个元素是树中的节点. 树中的每个节点有一个指向父节点的指针, 树节点的指针指向本身.
并查集支持两个操作:
- 合并 将两个子集合并成一个集合, 将一个子集的树的根节点指向另一个子集的树的根节点


- 查找 确定节点 v 属于那个子集, 从v开始一直向上寻找父节点, 直到树的根节点为止.
15.4.1 问题116: 朋友圈
有
n个城市,其中一些彼此相连,另一些没有相连。如果城市a与城市b直接相连,且城市b与城市c直接相连,那么城市a与城市c间接相连。省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个
n x n的矩阵isConnected,其中isConnected[i][j] = 1表示第i个城市和第j个城市直接相连,而isConnected[i][j] = 0表示二者不直接相连。返回矩阵中 省份 的数量。
示例 1:
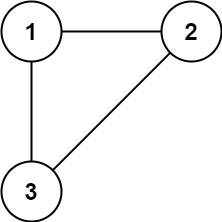
img 输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]] 输出:2示例 2:
img 输入:isConnected = [[1,0,0],[0,1,0],[0,0,1]] 输出:3提示:
1 <= n <= 200n == isConnected.lengthn == isConnected[i].lengthisConnected[i][j]为1或0isConnected[i][i] == 1isConnected[i][j] == isConnected[j][i]
15.4.1.1 分析&题解
若使用图的搜索算法, 需要避免重复搜索, 要将搜索过的节点进行标记, 可以使用深度和广度优先两种算法
广度优先搜索
图中有n个节点和n个边, TC 为 O()
func findCircleNum(isConnected [][]int) int {
// 访问标记
visited := make([]bool, len(isConnected))
res := 0
for i := range isConnected {
if !visited[i] {
bfs(isConnected, visited, i)
res++
}
}
return res
}
func bfs(isConnected [][]int, visited []bool, i int) {
// queue
q := []int{i}
visited[i] = true
for len(q) > 0 {
cur := q[0]
q = q[1:]
for j, n := range isConnected[cur] {
// 相连 && 未访问
if n == 1 && !visited[j] {
q = append(q, j)
visited[j] = true
}
}
}
}
并查集
n 个学生的朋友圈的图中有n个节点. 初始化时, 就有n个子图. 然后再将不同的节点连接起来形成独立的子图.
并查集的子集和图中的子图对应, 并查集中的子集用树形结构表示. 同一个子集的节点其根节点一定相同, 那么判断两个节点是否联通, 只需判断其是否有同一根节点.
查找:
创建长度为n的数组fathers存储n个节点的父节点. 那么对于节点i, 其根节点可以在数组内进行搜索, 时间复杂度为.
由于不关心父节点是什么, 只需要直到根节点即可, 那么在第一次找到根节点之后, 就将fathers[i]更新为根节点, 那么之后的时间复杂度为, 这种做法叫做路径压缩: 将长度为n的路径压缩到1.
合并: 只需将当前子集的根节点更新为另一子集的根节点即可.
func findCircleNum(isConnected [][]int) int {
// 初始化并查集
// 初始共有 n 个子集
n := len(isConnected)
fathers := make([]int, n)
for i := range fathers {
fathers[i] = i
}
// 扫描邻接矩阵
// 合并子集
res := n // 初始子集数
for i := range isConnected {
for j := range isConnected[i] {
// 如果相连 && 能够合并
if isConnected[i][j] == 1 && union(fathers, i, j) {
// 合并成功, 子集数减少
res--
}
}
}
return res
}
func union(fathers []int, i, j int) bool {
fatherOfI := findFather(fathers, i)
fatherOfJ := findFather(fathers, j)
// 合并
// 不属于同一子集
if fatherOfI != fatherOfJ {
fathers[fatherOfI] = fatherOfJ
return true
}
return false
}
func findFather(fathers []int, i int) int{
if fathers[i] != i {
// 寻找根节点
// 路径压缩
fathers[i] = findFather(fathers, fathers[i])
}
return fathers[i]
}
15.4.2 问题117: 相似字符串
如果交换字符串
X中的两个不同位置的字母,使得它和字符串Y相等,那么称X和Y两个字符串相似。如果这两个字符串本身是相等的,那它们也是相似的。例如,
"tars"和"rats"是相似的 (交换0与2的位置);"rats"和"arts"也是相似的,但是"star"不与"tars","rats",或"arts"相似。总之,它们通过相似性形成了两个关联组:
{"tars", "rats", "arts"}和{"star"}。注意,"tars"和"arts"是在同一组中,即使它们并不相似。形式上,对每个组而言,要确定一个单词在组中,只需要这个词和该组中至少一个单词相似。给定一个字符串列表
strs。列表中的每个字符串都是strs中其它所有字符串的一个 字母异位词 。请问strs中有多少个相似字符串组?字母异位词(anagram),一种把某个字符串的字母的位置(顺序)加以改换所形成的新词。
示例 1:
输入:strs = ["tars","rats","arts","star"] 输出:2示例 2:
输入:strs = ["omv","ovm"] 输出:1提示:
1 <= strs.length <= 3001 <= strs[i].length <= 300strs[i]只包含小写字母。strs中的所有单词都具有相同的长度,且是彼此的字母异位词。
15.4.2.1 分析&题解
判断单词和单词相似, 只需判断两者间不同字符的数量不超过两个即可.
func isSimilar(s1, s2 string) bool {
diffCnt := 0
for i := range s1 {
if s1[i] != s2[i] {
diffCnt++
}
}
return diffCnt <= 2
}
图的搜索
将单词作为节点, 相似则节点之间添加边, 构建图; 然后使用广度或深度优先搜索.
func numSimilarGroups(strs []string) int {
n := len(strs)
// 边界
if n == 1 {
return 1
}
// 邻接表
graph := make(map[string][]string, len(strs))
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
if isSimilar(strs[i], strs[j]) {
if _, ok := graph[strs[i]]; !ok {
graph[strs[i]] = []string{}
}
graph[strs[i]] = append(graph[strs[i]], strs[j])
}
}
}
// 访问标记
visited := make(map[string]bool, n)
res := 0
for _, str := range strs {
for !visited[str] {
bfs117(graph, visited, str)
res++
}
}
return res
}
func bfs117(graph map[string][]string, visited map[string]bool, str string) {
// Queue
q := []string{str}
visited[str] = true
for len(q) > 0 {
cur := q[0]
q = q[1:]
for _, adj := range graph[cur] {
if !visited[adj] {
q = append(q, adj)
visited[adj] = true
}
}
}
}
func isSimilar(s1, s2 string) bool {
difCnt := 0
for i := range s1 {
if s1[i] != s2[i] {
difCnt++
}
}
return difCnt <= 2
}
并查集
func numSimilarGroups(strs []string) int {
n := len(strs)
if n == 1 {
return 1
}
// 并查集
fathers := make([]int, n)
for i := range fathers {
fathers[i] = i
}
// 合并子集
res := n
for i := 0; i < n; i++ {
for j := i+1; j < n; j++ {
if isSimilar(strs[i], strs[j]) && union(fathers, i, j) {
res--
}
}
}
return res
}
func union(fathers []int, i, j int) bool {
fatherOfI := findFather(fathers, i)
fatherOfJ := findFather(fathers, j)
if fatherOfI != fatherOfJ {
fathers[fatherOfI] = fatherOfJ
return true
}
return false
}
func findFather(fathers []int, i int) int{
if fathers[i] != i {
fathers[i] = findFather(fathers, fathers[i])
}
return fathers[i]
}
func isSimilar(s1, s2 string) bool {
difCnt := 0
for i := range s1 {
if s1[i] != s2[i] {
difCnt++
}
}
return difCnt <= 2
}
15.4.3 问题118: 多余的边
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵
n个节点 (节点值1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在1到n中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为n的二维数组edges,edges[i] = [ai, bi]表示图中在ai和bi之间存在一条边。请找出一条可以删去的边,删除后可使得剩余部分是一个有着
n个节点的树。如果有多个答案,则返回数组edges中最后出现的边。示例 1:
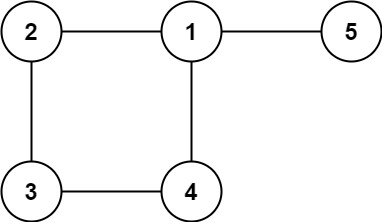
img 输入: edges = [[1,2],[1,3],[2,3]] 输出: [2,3]示例 2:
img 输入: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]] 输出: [1,4]提示:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ai < bi <= edges.lengthai != biedges中无重复元素- 给定的图是连通的
15.4.3.1 分析&题解
如果两个节点属于同一子集, 为两个节点添加边, 那么一定会形成环.
那么问题可以并查集来解决, 不断合并不同子集, 当出现节点所在两个子集无法合并时, 说明这两个节点在同一子集中, 此时为这两个节点添加边就会形成环.
func findRedundantConnection(edges [][]int) []int {
// 获取所有节点
maxVertex := math.MinInt
for _, r := range edges {
for _, n := range r {
maxVertex = max(maxVertex, n)
}
}
// 并查集
fathers := make([]int, maxVertex+1)
for i := 1; i < maxVertex+1; i++ {
fathers[i] = i
}
for _, r := range edges {
if !union(fathers, r[0], r[1]) {
return []int{r[0], r[1]}
}
}
return []int{}
}
func union(fathers []int, i, j int) bool {
fI := findFather(fathers, i)
fJ := findFather(fathers, j)
if fI != fJ {
fathers[fI] = fJ
return true
}
return false
}
func findFather(fathers []int, i int) int {
if fathers[i] != i {
fathers[i] = findFather(fathers, fathers[i])
}
return fathers[i]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
15.4.4 问题119: 最长连续序列
给定一个未排序的整数数组
nums,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。示例 1:
输入:nums = [100,4,200,1,3,2] 输出:4 解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1] 输出:9提示:
0 <= nums.length <= 10^4-109 <= nums[i] <= 10^9**进阶:**可以设计并实现时间复杂度为
O(n)的解决方案吗?
15.4.4.1 分析&题解
图的搜索
将每个数组看作节点, 差为1的数字间用边相连. 使用图的搜索算法找出所有子图的长度, 返回最大的即可
func longestConsecutive(nums []int) int {
set := make(map[int]bool, len(nums))
for _, n := range nums {
set[n] = true
}
var bfs func(map[int]bool, int) int
bfs = func(set map[int]bool, n int) int {
q := []int{n}
delete(set, n)
l := 1
for len(q) > 0 {
cur := q[0]
q = q[1:]
adjs := []int{cur-1, cur+1}
for _, adj := range adjs {
if set[adj] {
q = append(q, adj)
delete(set, adj)
l++
}
}
}
return l
}
res := 0
for _, n := range nums {
if len(set) > 0 {
res = max(res, bfs(set, n))
}
}
return res
}
func max(a, b int) int {
if a > b {
return a
}
return b
}